How To Create a Concrete Model for a Problem

01 Aug 2016

Perhaps the most misunderstood fact about young students is that they should not be taught algebra, because, for the most part, they do not ‘get’ it. Children in grades 1-4 should not be forced to retain algebraic models for solving a problem! Even though some of them are capable of thinking abstractly at a very early age, it is still extremely useful to wait and to use the time spent in the elementary grades building strong concrete comparison skills. At this age, children can develop the ability to solve problems by using, as the main tool, comparison of amounts. They can easily tell if an amount is larger, equal, or smaller than another amount. If the problem is solved using logical reasoning based on comparison, they have a much easier time understanding the solution and, of course, they learn much more naturally how to build a solution by themselves.

The purpose of this article is to teach parents and instructors how to approach problem solving from the perspective of a young student, who is in the concrete operational stage. This child can handle quantities that he can directly measure and compare. Problems should be approached by building a model that facilitates direct measurement and comparison. For example:

Problem: Father has given Andrew and Matthew equal amounts of money before they left for camp. Andrew has spent some of his money and now he has 8 dollars less than Matthew, who did not spend any. Together, they have 92 dollars left. How much money does Matthew have?

Solution: Make a box that represents the total amount. Divide it into two halves:

I have drawn it by hand to show you that it does not have to be drawn with a ruler and it does not have to be absolutely exact, but it does have to be visually clear that we mean for the two amounts of money to be equal.

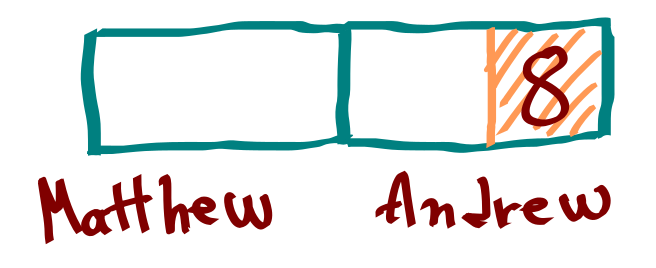
Take ‘8’ away from one of the halves. This is the amount that Andrew spent.

If you add back the money spent by Andrew, you get the amount they had been given at the start 92+8=100:

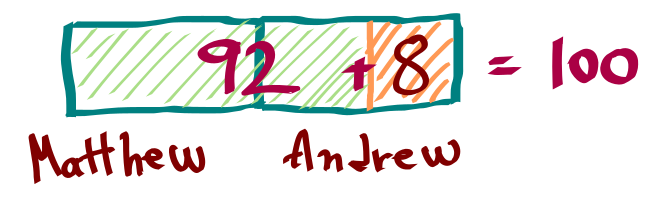
Split this into half to find out how much each was given 100=50+50.

Matthew has not spent any of his money and, therefore, he has 50 dollars.

Sometimes, it is not easy for the parent to come up with a model for such a problem that apparently can only be solved using a system of linear equations. In reality, most quality problems are thought up to have remarkably simple and cool models. Do not use algebra to solve them with young students! Even though it is easier for you to use algebra, for the student it is easier to understand this concrete approach. No matter how many times and in how much detail you will explain an algebraic approach, it will still not work as well. It is fun to build a concrete model and the student will understand much better how to figure out a solution on his own.

Our experience shows that solving problems using a concrete approach has its own cognitive benefits, enabling students to develop an ability for comparison of quantities that will remain useful for the rest of their life. Moreover, solving problems from an early age helps students develop those work habits that are very necessary, yet overlooked by schools: work discipline and self-organization, good observation of detail, capacity to take notes that summarize the data of the problem, ability to produce a decent drawing, and, most importantly, ability to think up a model and to illustrate it simply and efficiently. Students often lack the time to catch up on good work habits later on. We have extreme difficulty in the field with students who are smart, but cannot plan and execute a solution because: they write in a disorganized manner and are unable to make sense of their own calculations, they cannot make a figure for geometry based on a specification, they cannot focus for the time needed to finalize the solution, they do not have a sense of how to extract information from the data given by the statement, they cannot articulate an idea or a solution in order to collaborate with a group, etc.

For young students, we definitely recommend using concrete approaches to solutions. It is almost incredible how much problem solving can be done this way!